
그래프를 탐색하는 방법에는
깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)가 있음.
1. 깊이 우선 탐색(DFS)
: 최대한 깊이 내려간 뒤, 더 이상 깊이 갈 곳이 없을 경우 옆으로 이동
즉, 루트노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 모든 노드를 방문하고자 하는 경우 이 방법을 선택
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
- 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
2. 너비 우선 탐색(BFS)
: 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동
즉, 루트노드(혹은 다른 임의의 노드)에서 시작한 인접한 노드를 먼저 탐색하는 방법으로,
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택함
✴️ DFS/BFS 간단한 비교
- 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모름
- 너비 우선 탐색의 경우 - 나와 가까운 관계부터 탐색
깊이우선탐색(DFS) 너비우선탐색(BFS) 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색 현재 정점에 연결된 가까운 점들부터 탐색 스택(stack) 또는 재귀함수로 구현 큐(Queue)를 이용해서 구현
🔸DFS와 BFS의 시간복잡도
두 방식 모두 조건 내의 모든 노드를 탐색한다는 점에서 시간 복잡도는 동일함.
💡dfs, bfs에 가중치가 붙으면 사용할 수 없음
3. 최단거리 알고리즘
: 그래프 상에서 노드 간의 탐색 비용을 최소화하는 알고리즘
✏️다익스트라 알고리즘
- 가중치 그래프상에 존재하는 특정한 두 정점의 최단거리를 계산하는 알고리즘 (실제 자동차 네비에서 사용되는 알고리즘 중 하나)
- 그래프에서 간선 가중치의 합이 최소가 되는 경로를 찾는 알고리즘
- 가중치가 음수가 아닌 경우에만 사용가능
✏️밸만-포드 알고리즘
- 가중치 그래프에서 단일 출발점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘
- 음수 가중치에도 사용가능
✏️플로이드-와샬 알고리즘
- 가중치 그래프의 모든 쌍에 대해 최단 경로를 찾는 알고리즘
- 음수 가중치에도 사용가능
DFS와 BFS를 코드로 구현하여 그래프를 탐색해보자
1. DFS(깊이우선탐색)
두가지가 필요함
- visit list (방문한 노드를 체크하는 용도)
- 스택 (스택에 쌓아놓고 나중에 POP해서 출력함) : LIFO(LAST IN FIRST OUT)
2. 코드 구현 (중요도🌟🌟🌟🌟)
DFS를 iterative로 구현하거나 재귀로 구현하는 방식 두 가지를 해보자
보통 그래프를 코드로 구현할 때 딕셔너리 또는 이차행렬로 구현함.

iterative_dfs (while 반목문으로) 코드 구현하는 순서
visit list 만들기 (빈 리스트 생성)
stack 만들기 (처음 들어가는 노드를 스택에 넣는다.)
while 반복문 (모든 노드를 탐색하기 위해) (이때 스택이 비어질 때까지 반복함)
스택에 있는 노드를 꺼낸다(내 손에 노드가 쥐어져있다고 생각하자)
꺼낸 노드가 방문리스트에 있는지 확인
방문리스트에 없다면 노드를 방문리스트에 추가한다. (방문 순서를 알 수 있게 됨)
현재 노드와 인접하는 노드를 꺼내어 스택에 쌓는다
(while문에 의해) pop한 노드가 방문 여부 확인
만약 방문한 노드라면 다른 노드를 pop함
이전과 동일하게 꺼낸 노드와 인접한 노드 중 방문하지 않은 노드를 찾는다
만약 모든 노드를 방문했을 경우 스택에 쌓여있는 노드들이 하나씩 pop 한다
스택이 empty가 되면 코드는 종료된다

🫧visit list를 만드는 두 가지 방법
1. visit 배열을 0으로 만들어놓고 방문하면 1로 체크하는 방법
2. visit 배열을 빈 리스트로 만들어놓고, 방문한 노드를 append 하는 방법 (방문순서를 알 수 있게 됨)
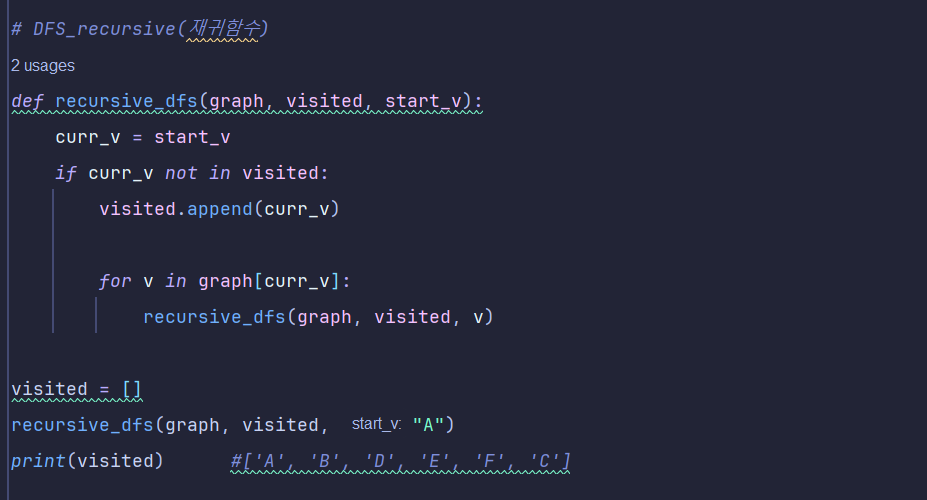
recursive_dfs (재귀함수로) 코드 구현하는 순서
visit list 만들기 (빈 리스트 생성) : 이때 주의할 점, 재귀함수 안에 visit 리스트를 생성하면 함수가 재귀될 때마다 리스트가 초기화 되기 때문에, 함수 밖에 빈 리스트를 선언한다. (좋은 코드는 함수 인자 값으로 빈 리스트를 받도록 함)
현재 꺼낸 노드를 받는 값을 설정해준다. (내 손에 쥐고 있는 노드)
꺼낸 노드가 방문리스트에 있는지 확인
방문리스트에 없다면 노드를 방문리스트에 추가한다. (방문 순서를 알 수 있게 됨)
현재 노드와 인접하는 노드를 꺼내고
인접하는 노드를 재귀함수에 넣는다.
재귀함수에 들어간 노드와 인접하는 노드를 반환하는 것을 계속 반복한다
만약 모든 노드를 방문했을 경우 재귀(스택)에 쌓여있는 노드들이 하나씩 반환된다.
재귀에 쌓여있는 값들이 모두 반환됐을 경우, 자동 종료된다.
3. DFS를 사용하는 용도
- 경로 탐색(최단경로 찾는 게 아니라 경로가 있는지)
- 사이클 검출
- 그래프 연결성 확인
+) DFS를 하면 신장트리를 만들 수 있음
4. BFS(넓이우선탐색)
두가지가 필요함
- visit list (방문한 노드를 체크하는 용도)
- 큐 : FIFO(FIRST IN FIRST OUT)
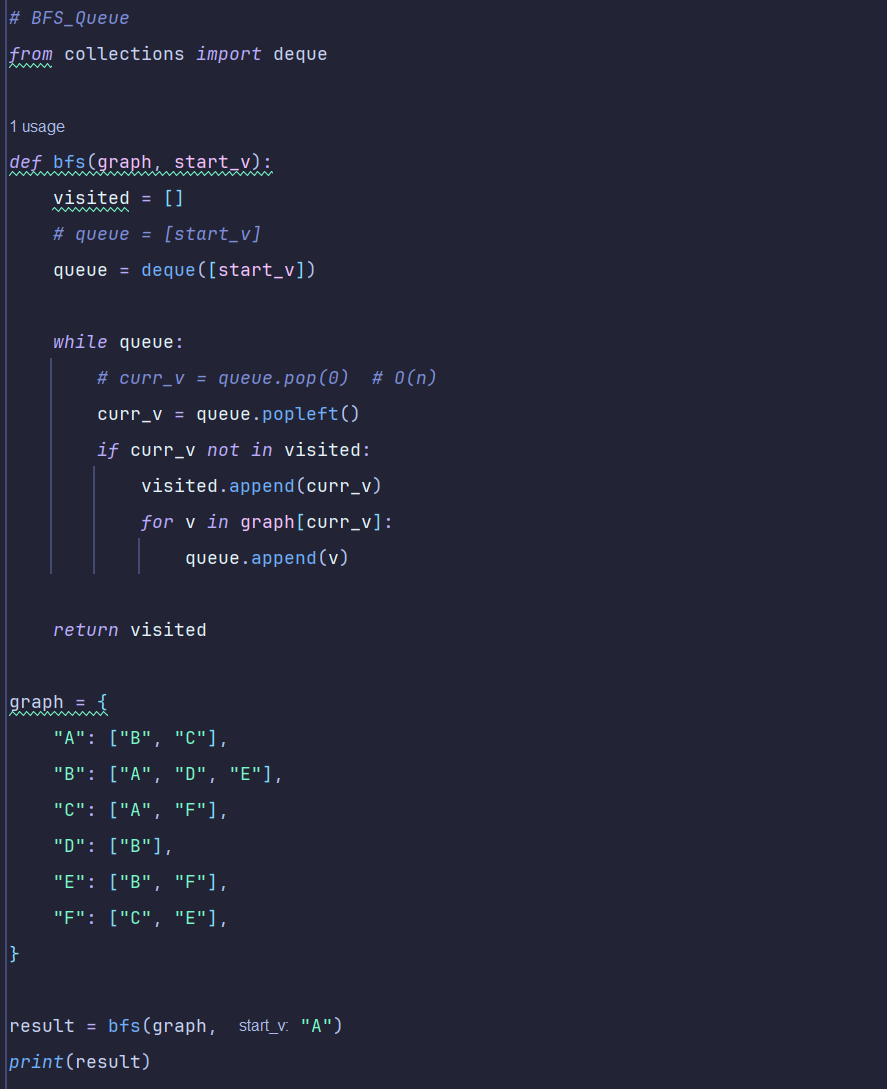
5. 코드 구현 (중요도🌟🌟🌟🌟)
6. BFS를 사용하는 용도
- 최단 경로 탐색할 때는 BFS가 더 유리함
- 연결 요소 탐색
- 그래프 전체 탐색
📍deque?
큐(Queue) : The order of arrival (줄서기)
데크(deque) : 양방향 큐
==> 앞, 뒤 방향에서 element를 추가하거나 삭제할 수 있음
[아래 용어가 나오면 큐임]
REAR : 데이터가 삽입되는 곳(인덱스라고 생각하면 됨) (스택에선 TOP)
처음에는 rear랑 front의 지점이 같음. 값이 추가될 수록 rear가 한칸씩 앞으로 감
이때 큐의 끝까지 다 갔다면, full of queue 인 거 (queue의 전체 size-1한 값이 rear라면 full인 거 : rear == size - 1)
FRONT : 데이터가 삭제되는 곳(인덱스라고 생각하면 됨)
deque를 하게 되면, front의 위치가 한칸씩 앞으로 가게 됨.
AddQ : 데이터 넣을 때 (스택에선 PUSH)
DeleteQ : 데이터를 삭제 반환할 때 (스택에선 pop)
(add - remove, enqueue - dequeue)
📁 추가 내용
rear == size - 1 이면 queue 는 full 한 상태라고 나타냄. (deque를 해서 모두 값이 없는데도 full 이라고 말함)
그래서, 두가지의 스페셜 큐를 만들어냄.
- Circular queue: (rear와 front의 출발지점이나 도착지점이 모두 같음 즉 운동장 트랙같은 느낌)
- doubley-Ended Queue: rear와 front 모두 삽입과 삭제를 할 수 있게 하는 큐
Queue 시간복잡도
- deque는 양쪽 끝에서의 삽입과 삭제 연산(popleft)이 평균적으로 O(1)
- 파이썬의 리스트의 pop(0) 시간복잡도가 O(n)
(bc) 파이썬에 리스트는 연결리스트가 아닌 동적배열임.
큐의 First가 Out하면[FIFO] , 리스트 안의 element가 앞으로 한칸씩 이동함. 즉, 시간복잡도 O(n)
==> 즉, DEQ를 사용하면, 조금 더 빠르게 코드를 구현할 수 있음. (시간복잡도 O(1))
📍 deque 사용법
from collections import deque
deque.append(item): item을 데크의 오른쪽 끝에 삽입한다.
deque.appendleft(item): item을 데크의 왼쪽 끝에 삽입한다.
deque.pop(): 데크의 오른쪽 끝 엘리먼트를 가져오는 동시에 데크에서 삭제한다.
deque.popleft(): 데크의 왼쪽 끝 엘리먼트를 가져오는 동시에 데크에서 삭제한다.
deque.extend(array): 주어진 리스트를 데크의 오른쪽에 추가한다.
deque.extendleft(array): 주어진 리스트를 데크의 왼쪽에 추가한다.
deque.remove(item): item을 데크에서 찾아 삭제한다. (제일 처음 나온 해당 string만 제거됨)
deque.clear(): 해당 deque 전체 삭제
deque.reverse(): 말그대로 역순으로 정렬한다.
deque.rotate(num): 데크를 num만큼 회전한다(양수면 오른쪽, 음수면 왼쪽).
'알고리즘' 카테고리의 다른 글
| 자료구조 (선형/비선형) (0) | 2024.08.09 |
|---|---|
| 시간 복잡도와 공간 복잡도 (0) | 2024.08.07 |
| 자료구조_그래프 +)신장트리, 최소신장트리 (0) | 2024.07.31 |
| 자료구조_트리 (0) | 2024.07.29 |
| 알고리즘 기초_stack(스택) (0) | 2024.07.11 |