minjoo0613 님의 블로그

자료구조

✨자료구조에서는 데이터랑 연산이 꼭 필요함

선형 자료구조(Linear Data Structure)

: 데이터 요소를 순서대로 정렬

✨ 개별 요소에 접근하는 작업에는 선형 자료구조가 더 효율적.

선형 자료구조에서는 첫 번째 요소가 마지막 요소까지 백트래킹(Backtracking)없이 순회할 수 있지만, 비선형 자료구조에서는 종종 되돌아가야 함.

배열(Array)

배열의 가장 큰 특징은 인덱스 (추가, 삭제, 삽입, 수정)

✨특징

- 선형 자료구조(1차원 자료구조)
- 모든 요소는 동일한 데이터 타입을 가짐

- 정적 자료구조 : 크기가 고정되어 있는 자료구조
- 각 요소는 하나의 인덱스에 매핑
- 고정된 크기를 가짐
- 연속된 메모리 블럭에 할당(메모리 한 칸의 크기가 모두 동일함)
- 정렬되어있기 때문에, 빅오 속도를 더 빠르게 할 수 있음 (O(log n) -> 이분탐색
- 기본적으로 시간복잡도 O(1)

✨시간복잡도 연산

삽입/수정/삭제 ==>  O(n)

연결 리스트(Linked list)

연결리스트는 인덱스가 없음. 첫 번째 노드의 값을 읽어서 다음 노드의 주소를 찾아야 됨

메모리 안에 랜덤하게 배정하여 노드가 그 주소를 가지고 있음.

✨특징

- 선형 자료구조(1차원 자료구조)
- 모든 요소는 동일한 데이터 타입을 가짐

- 동적 자료구조 : 크기가 바뀔 수 있는 자료구조
- 첫 번째 노드의 주소만 알고 있음
- 가변 크기를 가질 수 있음
- 비연속된 메모리 블럭에 할당
- 연결리스트는 불연속이라 빅오가 더 빨라질 방법은 없음

파이썬은 배열과 연결리스트 특징을 모두 가지고 있음
그래서 동적 배열이라고 부름.(Dynamic Array)

비선형 자료구조(Nonlinear Data Structure)

: 데이터를 비연속적으로 연결

트리(Tree)와 그래프(Graph)

트리는 계층 구조가 있는 가계도, 조직도에 주로 쓰임
그래프는 SNS와 같이 한 사람의 영향력을 네트워크처럼 표현

트리를 연산할 때 필요한 것 : 추가, 삭제, 수정, 정렬, 탐색(계층 아래까지 갔다가 다음 계층으로 이동해서 아래로 팜)
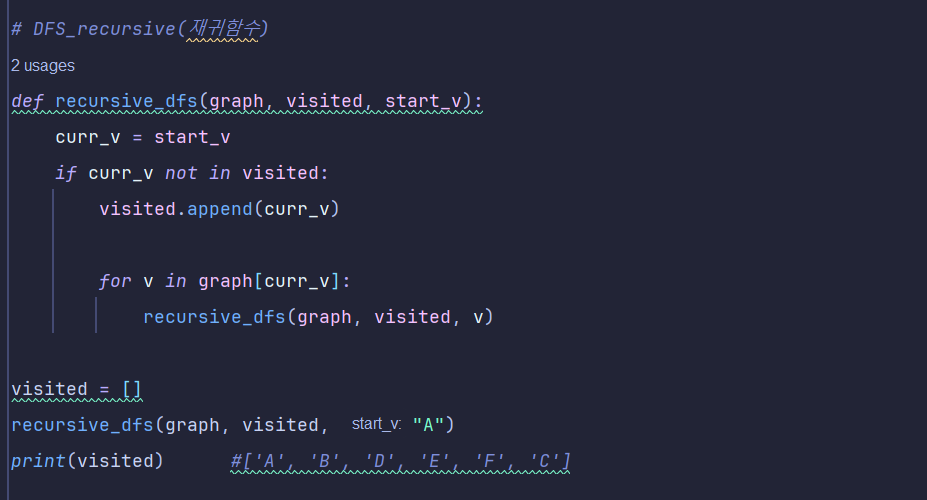
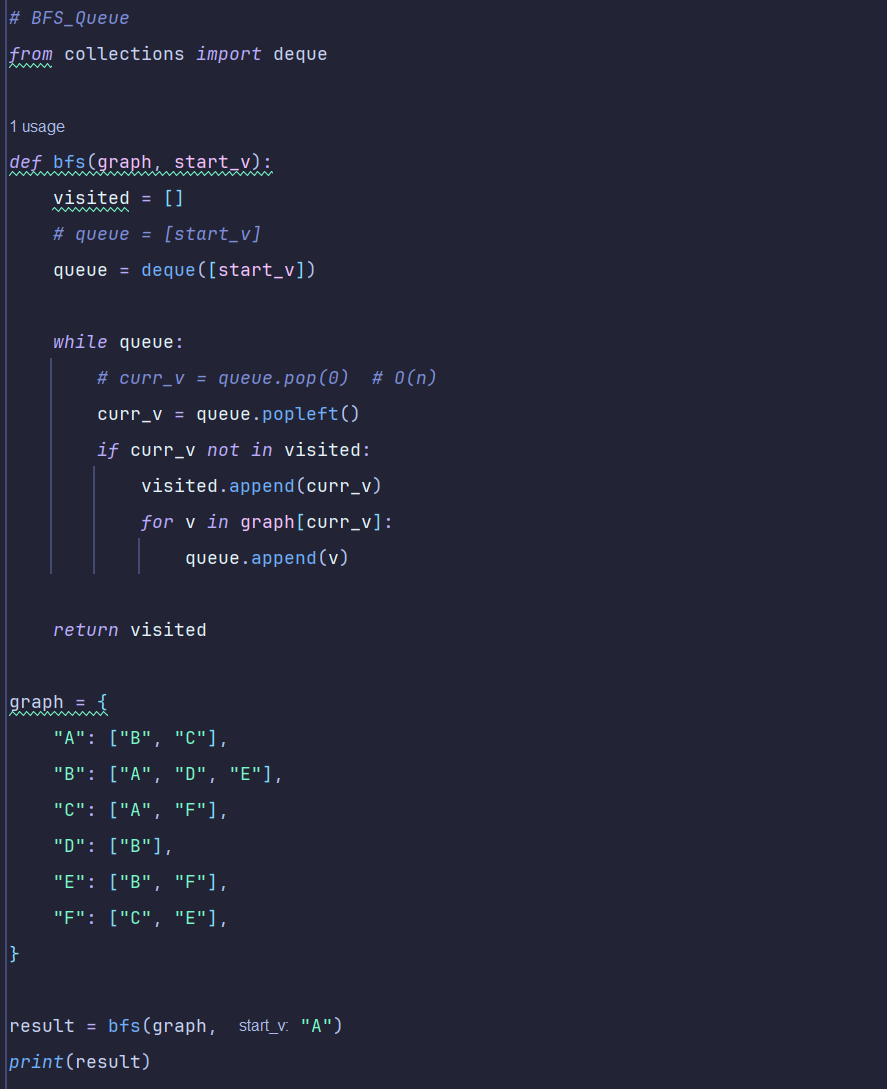
그거를 DFS(깊이 우선 탐색), BFS(너비 우선 탐색) -> 탐색하는 알고리즘

트리랑 그래프 자료구조에서 대표적인 알고리즘이 dfs, bfs 임

Search or Retrieve

Search : 검색하다

get an index from an element

- 보통 특정 원소(요소)의 위치(인덱스)를 찾는 과정.
- 위치(인덱스)를 알고 있지 않음
- 찾는 것

✨ 선형 탐색 : 정렬되지 있지 않은 배열에서 for문으로 하나씩 돌면서 인덱스 값 도출
✨ 이진 탐색(이분 탐색) : 정렬된 배열에서 가능, 이분 즉 반씩 범위를 좁혀가며 인덱스 값 도출

분할 정복 기법 (이 안에 이진 탐색이 들어감)

: 큰 문제를 작은 문제들로 쪼개서 작은 문제들을 해결하는 것으로 큰 문제를 해결하는 기법, 3가지

- divide : 큰 문제를 작은 문제로 쪼갬
- conquer : 작은 문제들에서 결론을 도출해내는 과정 (재귀로 띄고 있는 경우가 많다)
- combine(optional) : 있을수도 있고, 없을 수도 있음

✨ 대표적인 분할 정복 예시 (토너먼트): 이분 탐색, 병합 정렬, 퀵 소트

### 알고리즘 공부하려면 토익처럼, ⓐ문자열(회문, 파문) ⓑ배열 순회

Retrive : 검색하다(가져오다)

get an element from an index

- 특정 인덱스나 위치에서 해당하는 원소(요소)를 가져오는 과정
- 이미 인덱스나 위치를 알고 있음.
- 가져오는 것

시간 복잡도와 공간 복잡도

복잡도란, 알고리즘의 성능, 효율성을 나타내는 척도를 말함

각 알고리즘이 주어진 특정 크기의 입력(n)을 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준을 제시함.

알고리즘을 평가할 때 주로 수행 시간과 메모리 사용량을 기준으로 두는데, 이 중 수행 시간에 해당하는 것이 시간 복잡도이고 메모리 사용량에 해당하는 것이 공간 복잡도이다.

시간 복잡도(Time Complexity)

특정 크기의 입력을 기준으로 할 때 필요한 연산의 횟수를 나타냄.

공간 복잡도(Space Complexity)

프로그램 실행과 완료에 얼마나 많은 공간(메모리)가 필요한지를 나타냄

시간 복잡도와 공간 복잡도는 반비례하는 경향이 있어, 보통 알고리즘의 성능을 판단할 때는 시간 복잡도를 위주로 판단함

어떻게 하면 더 효율적으로 해결할 수 있을까?

해결책을 비용으로 나눈 것을 퍼포먼스라고 하고, 이 퍼포먼스를 올리기 위함

Solution (대전제: No Solution, no performance)
알고리즘이고 뭐고 일단 문제를 해결할 수 있는 방법을 찾아야 한다.

퍼포먼스를 올리려면, 서버 비용을 낮춰야 됨

- Temporal Resource 시간 자원
CPU : 겁나 빠른 계산기(CPU가 열심히 계산해서 결과를 도출하는 게 시간과 연관이 있음)

- Spatial Resource 공간 자원
메모리를 얼만큼 쓰는가
주 저장장치(램=메모리), 보조 저장장치(SSD, USB)
램은 SSD에 비해 100배 이상 빠름

★Key point1: Performance of worst case is important(최악의 경우가 중요함)

CS에서의 비용이란?
공간 복잡도, 시간 복잡도 
공간의 기술이 좋아지면서, 공간 복잡도가 크게 중요하지 않게 됨.
(중요한 건 시간의 비용이다)

★Key point2: Performace of time is important(시간이 중요함)

내 프로그램이 최악일 때, f(n)이 어디로 향할까
worst case는 n이 엄청 커질 때임(n이 무한으로 갈 때)
최악의 경우가 어디까지 도달하냐

점근적 복잡도 : 알고리즘의 성능을 나타내는 척도
주로 입력(n)의 크기가 무한히 커질 때 알고리즘의 성능이 어떻게 변하는지를 분석
즉 알고리즘의 성능은 주어진 문제의 입력 크기에 따라 달라짐

입력이 n이라면 성능은 f(n)이라 할 수 있음
f(n)은 입력 크기 n에 대한 알고리즘의 시간(공간) 복잡도를 나타내는 함수

★Key point3: Performace is a function of input size(인풋 사이즈가 중요함)

우리의 목표는 알고리즘의 성능이 얼마나 좋은지 가늠하고 싶을 뿐(정확한 수치 도출이 아님)
즉, 비교를 통해 짐작을 하고 싶은 거

★Key point4: Some key functions are used for standards (여러 비교 대상의 기준이 필요함)

f(n)의 정확한 값이 필요한 게 아니라 어떤 값과 비교했을 때 더 빠른지, 느린지 비교가 하고 싶은 것.

즉, g(n) 설정해두면 g(n)가 f(n)을 비교하여 크기를 비교할 수 있음.

빅오 "표기법": 큰 동그라미 표기법

> 입력값이 커질 때 알고리즘의 실행 시간(시간 복잡도) 혹은 공간 요구사항(공간 복잡도)가 어떻게 증가하는지 '분류' 혹은 '비교'하는데 유용하게 사용되는 표기법
최고 차항만을 표기, 계수는 무시 (어차피 n은 무한대로 보내니까)

시간복잡도는 O(n^2) : 입력값(n)에 따른 알고리즘의 점근적 추이가 n^2 함수의 모양처럼 올라감
== 입력값(n)에 따른 알고리즘의 실행시간의 추이가 n^2처럼 생겼다

[★Key functions★]

O(1) 상수 시간 복잡도: 입력값이 아무리 커도 실행시간이 일정함 (가장 좋은 알고리즘)
>상수시간복잡도로 해시 테이블의 조회와 삽입 연산이 있음

O(log n)로그 시간 복잡도: 매우 큰 값에도 영향을 받지 않아서 큰 값을 다루는 학문에서 자주 쓰임 (이분 탐색)(점점 반으로 줄여서 찾음)
로그는 매우 큰 값에도 영향을 많이 받지 않음
+)배열에서 정렬이 된 경우라면 빅오는 O(log n)이 됨

O(n) 선형 시간 복잡도: 입력값만큼 비례해서 실행 시간에 영향을 받음(한 개의 for문 이에 해당)
> 정렬되지 않은 리스트에서 최댓값 또는 최솟값을 찾는 경우
> 배열(array) 기본적으로 O(n)

O(n log n): 병합 정렬을 비롯한 대부분의 효율 좋은 정렬 알고리즘이 이에 해당

-------------------------------------------------------- (▼inefficiency▼) ---------------------------------------------------------

O(n^2): 버블 정렬 같은 비효율적인 정렬 알고리즘 (중복 for문이 이에 해당)

O(2^n): 피보나치의 수를 재귀로 계산하는 알고리즘이 이에 해당

O(n!): 굉장히 효율이 안 좋은 알고리즘

★빅오를 구할 때는, 로직 한 줄씩 모두 이해해야 구할 수 있음(즉 코드를 이해해야 됨)

그래프를 탐색하는 방법에는

깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)가 있음.

1. 깊이 우선 탐색(DFS)

: 최대한 깊이 내려간 뒤, 더 이상 깊이 갈 곳이 없을 경우 옆으로 이동
즉, 루트노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법

- 모든 노드를 방문하고자 하는 경우 이 방법을 선택

- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함

- 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림

2. 너비 우선 탐색(BFS)

: 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동
즉, 루트노드(혹은 다른 임의의 노드)에서 시작한 인접한 노드를 먼저 탐색하는 방법으로,
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

- 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택함

✴️ DFS/BFS 간단한 비교
- 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모름
- 너비 우선 탐색의 경우 - 나와 가까운 관계부터 탐색

깊이우선탐색(DFS)	너비우선탐색(BFS)
현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색	현재 정점에 연결된 가까운 점들부터 탐색
스택(stack) 또는 재귀함수로 구현	큐(Queue)를 이용해서 구현

🔸DFS와 BFS의 시간복잡도
두 방식 모두 조건 내의 모든 노드를 탐색한다는 점에서 시간 복잡도는 동일함.


💡dfs, bfs에 가중치가 붙으면 사용할 수 없음

3. 최단거리 알고리즘

: 그래프 상에서 노드 간의 탐색 비용을 최소화하는 알고리즘

✏️다익스트라 알고리즘
- 가중치 그래프상에 존재하는 특정한 두 정점의 최단거리를 계산하는 알고리즘 (실제 자동차 네비에서 사용되는 알고리즘 중 하나)

- 그래프에서 간선 가중치의 합이 최소가 되는 경로를 찾는 알고리즘
- 가중치가 음수가 아닌 경우에만 사용가능

✏️밸만-포드 알고리즘
- 가중치 그래프에서 단일 출발점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘
- 음수 가중치에도 사용가능

✏️플로이드-와샬 알고리즘
- 가중치 그래프의 모든 쌍에 대해 최단 경로를 찾는 알고리즘
- 음수 가중치에도 사용가능

DFS와 BFS를 코드로 구현하여 그래프를 탐색해보자

1. DFS(깊이우선탐색)
두가지가 필요함
- visit list (방문한 노드를 체크하는 용도)
- 스택 (스택에 쌓아놓고 나중에 POP해서 출력함) : LIFO(LAST IN FIRST OUT)

2. 코드 구현 (중요도🌟🌟🌟🌟)

DFS를 iterative로 구현하거나 재귀로 구현하는 방식 두 가지를 해보자

보통 그래프를 코드로 구현할 때 딕셔너리 또는 이차행렬로 구현함.

iterative_dfs (while 반목문으로) 코드 구현하는  순서

visit list 만들기 (빈 리스트 생성)
stack 만들기 (처음 들어가는 노드를 스택에 넣는다.)

while 반복문 (모든 노드를 탐색하기 위해) (이때 스택이 비어질 때까지 반복함)
스택에 있는 노드를 꺼낸다(내 손에 노드가 쥐어져있다고 생각하자)
꺼낸 노드가 방문리스트에 있는지 확인
방문리스트에 없다면 노드를 방문리스트에 추가한다. (방문 순서를 알 수 있게 됨)

현재 노드와 인접하는 노드를 꺼내어 스택에 쌓는다
(while문에 의해) pop한 노드가 방문 여부 확인
만약 방문한 노드라면 다른 노드를 pop함

이전과 동일하게 꺼낸 노드와 인접한 노드 중 방문하지 않은 노드를 찾는다
만약 모든 노드를 방문했을 경우 스택에 쌓여있는 노드들이 하나씩 pop 한다
스택이 empty가 되면 코드는 종료된다

🫧visit list를 만드는 두 가지 방법
1. visit 배열을 0으로 만들어놓고 방문하면 1로 체크하는 방법
2. visit 배열을 빈 리스트로 만들어놓고, 방문한 노드를 append 하는 방법 (방문순서를 알 수 있게 됨)

recursive_dfs (재귀함수로) 코드 구현하는 순서

visit list 만들기 (빈 리스트 생성) : 이때 주의할 점, 재귀함수 안에 visit 리스트를 생성하면 함수가 재귀될 때마다 리스트가 초기화 되기 때문에, 함수 밖에 빈 리스트를 선언한다. (좋은 코드는 함수 인자 값으로 빈 리스트를 받도록 함)

현재 꺼낸 노드를 받는 값을 설정해준다. (내 손에 쥐고 있는 노드)
꺼낸 노드가 방문리스트에 있는지 확인
방문리스트에 없다면 노드를 방문리스트에 추가한다. (방문 순서를 알 수 있게 됨)

현재 노드와 인접하는 노드를 꺼내고
인접하는 노드를 재귀함수에 넣는다.
재귀함수에 들어간 노드와 인접하는 노드를 반환하는 것을 계속 반복한다

만약 모든 노드를 방문했을 경우 재귀(스택)에 쌓여있는 노드들이 하나씩 반환된다.
재귀에 쌓여있는 값들이 모두 반환됐을 경우, 자동 종료된다.

3. DFS를 사용하는 용도
- 경로 탐색(최단경로 찾는 게 아니라 경로가 있는지)
- 사이클 검출
- 그래프 연결성 확인

+) DFS를 하면 신장트리를 만들 수 있음

4. BFS(넓이우선탐색)
두가지가 필요함
- visit list (방문한 노드를 체크하는 용도)
- 큐 : FIFO(FIRST IN FIRST OUT)

5. 코드 구현 (중요도🌟🌟🌟🌟)

6. BFS를 사용하는 용도
- 최단 경로 탐색할 때는 BFS가 더 유리함
- 연결 요소 탐색
- 그래프 전체 탐색

📍deque?
큐(Queue) : The order of arrival (줄서기)
데크(deque) : 양방향 큐
==> 앞, 뒤 방향에서 element를 추가하거나 삭제할 수 있음

[아래 용어가 나오면 큐임]
REAR : 데이터가  삽입되는 곳(인덱스라고 생각하면 됨) (스택에선 TOP)
처음에는 rear랑 front의 지점이 같음. 값이 추가될 수록 rear가 한칸씩 앞으로 감
이때 큐의 끝까지 다 갔다면, full of queue 인 거 (queue의 전체 size-1한 값이 rear라면 full인 거 : rear == size - 1)

FRONT : 데이터가 삭제되는 곳(인덱스라고 생각하면 됨)
deque를 하게 되면, front의 위치가 한칸씩 앞으로 가게 됨.

AddQ : 데이터 넣을 때 (스택에선 PUSH)

DeleteQ : 데이터를 삭제 반환할 때 (스택에선 pop)
(add - remove, enqueue - dequeue)

📁 추가 내용

rear == size - 1 이면 queue 는 full 한 상태라고 나타냄. (deque를 해서 모두 값이 없는데도 full 이라고 말함)

그래서, 두가지의 스페셜 큐를 만들어냄.
- Circular queue:  (rear와 front의 출발지점이나 도착지점이 모두 같음 즉 운동장 트랙같은 느낌)
- doubley-Ended Queue: rear와 front 모두 삽입과 삭제를 할 수 있게 하는 큐

Queue 시간복잡도
- deque는 양쪽 끝에서의 삽입과 삭제 연산(popleft)이 평균적으로 O(1)
- 파이썬의 리스트의 pop(0) 시간복잡도가 O(n)

(bc) 파이썬에 리스트는 연결리스트가 아닌 동적배열임.

큐의 First가 Out하면[FIFO] , 리스트 안의 element가 앞으로 한칸씩 이동함. 즉, 시간복잡도 O(n)

==> 즉, DEQ를 사용하면, 조금 더 빠르게 코드를 구현할 수 있음. (시간복잡도 O(1))

📍 deque 사용법

from collections import deque

deque.append(item): item을 데크의 오른쪽 끝에 삽입한다.
deque.appendleft(item): item을 데크의 왼쪽 끝에 삽입한다.
deque.pop(): 데크의 오른쪽 끝 엘리먼트를 가져오는 동시에 데크에서 삭제한다.
deque.popleft(): 데크의 왼쪽 끝 엘리먼트를 가져오는 동시에 데크에서 삭제한다.
deque.extend(array): 주어진 리스트를 데크의 오른쪽에 추가한다.
deque.extendleft(array): 주어진 리스트를 데크의 왼쪽에 추가한다.
deque.remove(item): item을 데크에서 찾아 삭제한다. (제일 처음 나온 해당 string만 제거됨)
deque.clear(): 해당 deque 전체 삭제
deque.reverse(): 말그대로 역순으로 정렬한다.
deque.rotate(num): 데크를 num만큼 회전한다(양수면 오른쪽, 음수면 왼쪽).

그래프

1. 그래프의 약자

Graph(그래프)
Graph : G = (V, E) 이 두개가 세트임
V: vertex (트리에선 노드)
E: a set of pairs of nodes (엣지)
▼▼▼▼▼▼▼▼▼▼
V = {0,1,2,3}
E = {(0,1), (0,2), (0,3), (1,2), (1,3), (2,3)}
u: tail of the edge
v: head of the edge
<u, v> =/= <v, u>

2. 방향/무방향 그래프

양방향(무방향) 그래프: <u, v> == <v, u>
단방향(방향) 그래프: <u, v> =/= <v, u>

그래프에서 (1,1)이 있다면, 자신이 자신에게로 향한 것임(그런 그래프도 있을 수 있음)

3. 그래프의 용어 (중요도 🌟 🌟)

🔸사이클(cycle): 시작 정점과 종료 정점이 같은 단순 경로 (그런 그래프를 사이클이 있는 그래프라고 부름)

🔸인접성(adjacency): 그래프에서 두개의 정점이 간선으로 직접 연결되어 있다면 인접하다고 말함. (그냥 서로 선이 연결돼있으면 인접한거)

🔸경로(path): 시작 정점에서 종료 정점까지 가는 다양한 경로
이때 다양한 경로가 존재할 수 있다 == length of path 가 다를 수 있음 (짧은 경로가 있을 수 있고, 긴 경로가 있을 수 있음)

🔸연결(Connected): 어떤 노드로 다른 노드로 갈 수 있느냐를 봤을 때, 갈 수 있다면 연결되어있다고 말함
(즉 연결되어있지 않는 그래프가 있을 수 있음. 중간에 경로가 끊긴 겨)

🔸가중치(weight): 지도로 따지자면 하나의 경로에 걸리는 시간이 가중치라고 생각하면 됨. 경로에 부하된 가중치가 있음.

그 가중치로 최단의 경로를 제시해줌. 거리가 짧다고 가중치가 낮다고 볼 수 없음.

4. 트리는 그래프 중 하나

: 트리도 그래프 중 하나이고, 특정한 조건을 만족하여 트리라고 부르는 것

그 조건은,
두 개의 노드 사이에 반드시 1개의 경로만 가지면서, 사이클이 존재하지 않는 방향 그래프
(방향이 위에서 아래로 떨어지는 상하 그래프)

5. 신장트리(Spanning Tree)

: 모든 정점을 포함하지만 모든 엣지를 포함하고 있지는 않으며, 사이클이 없는 연결 그래프

(즉 그래프가 모두 간선으로 이어져있지는 않음)

6. 최소신장트리(Minimum Spanning Tree, MST)

: 신장 트리 중에서도 간선의 가중치 합이 최소가 되는 신장트리를 말함.
MST는 실제로 네트워크 설계, 도로망 구축 등에서 비용을 최소화하기 위해 굉장히 많이 사용

최소신장트리의 알고리즘(일단 지금은 중요하지 않으니 용어만 알아두기)
크루스칼 알고리즘: 모든 간선을 가중치 순으로 정렬한 후 스패닝 트리를 구하는 방법
프림 알고리즘: 시작 정점에서 출발해서 최소 가중치의 간선을 선택하며 트리를 확장해 나가는 방법

7. 그래프를 구현하는 2가지 방법 (중요도 🌟 🌟 🌟 )

- 인접 행렬: 

방향그래프인지, 무방향 그래프에 따라 인접행렬이 달라짐. 무방향 그래프일 경우 인접 행렬은 대칭을 이루게 됨

장점: 행렬이기 때문에 사용하기 편할 수 있음. 근데 행이나 열이 너무 많아지면 표를 나타내는 공간을 많이 차지하기 때문에 쓰기가 어려움 (공간복잡도)

- 인접 리스트: 

연결리스트처럼 표현함

장점: 공간을 덜 차지함 (vertex가 많을 때 인접리슽를 사용하면 좋음)

📁 추가 내용

우리의 관심사는 '순회'임
즉, 주어진 그래프의 특정 정점에서 도달 가능한 모든 정점을 찾는 것
DFS, BFS

DFS(깊이우선탐색) 코드 구현하는 방법 (요약)

탐색할 때 마킹을 해야 함. (해당 vertex는 방문했다는 표시, 즉 표시할 리스트가 필요함)
나랑 인접한 vertex 중에 하나 선택해서 방문함. 그리고 방문하지 않은 vertex로 감
스택에 쌓는다
만약 이미 방문했을 경우 pop한다.(back 한다)
모두 방문했을 경우, 스택에 쌓인 걸 순서대로 pop한다

📌 선형 자료구조(Linear Data Structure)

일반적으로는 배열(array), 연결리스트
파이썬에서는 리스트, 튜플, 큐, 스택

하나의 자료 뒤에 하나의 자료만 있음

🔸특징

- 일직선으로 연결되어 있음
- 이전 - 현재 - 다음 (연속성)
- 각각 요소들이 매핑되어있음

🔸한계점

선형으로된 자료만 표현할 수 있음 == 계층에 대한 표현이 불가함

📌 비선형 자료구조(NonLinear Data Structure)

하나의 자료 뒤에 여러 개의 자료가 있을 수 있음

데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조

계층형 자료구조

🔸 특징

- 한 가지의 소스에서 연결되어 있음
- 하나의 노드가 여러 노드로 전파됨
- 순환구조가 없음 (중요도 🌟🌟🌟)    (단순 순환을 갖지 않고, 연결된 무방향 그래프 구조임)

👉이걸 '트리'라고 함

🔸 조건

🥕조건 01
Node (or Vertes) : 값을 가지고 있는 기본 단위 객체
Edge : 상위 노드와 하위 노드 간의 연결하는 선(link)

🥕조건 02
Root : 트리의 맨 위에 있는 노드, 유일한 부모가 없는 노드
Leaf : 더 이상 자식 노드가 없는 최하위 노드
Internal : root와 left 사이의 내부 노드 

🥕조건 03
Parent : 해당 노드 바로 위에 있는 부모 노드
Child : 해당 노드 바로 아래에 있는 자식 노드
Sibling :동일한 부모를 가지고 있는 노드들

🥕조건 04
ancestor(each node -> root node) : 조상 노드
diancestor(root node -> each node) : 자손 노드

🥕조건 05
Sub Tree : 주어진 노드의 모든 하위 목록 (그 계층을 삼각형 틀로 보면 됨. ex. 나, 금쪽이, 우리 아빠)

🥕조건 06 (중요도🌟🌟🌟)
🌟degree of a node : 특정 노드가 가지고 있는 자식 노드의 수 (주의, 자식과 자손은 다름. 자손은 포함하지 않음)
🌟degree of a tree : 가장 높은 차수를 가진 노드의 차수(즉, 특정 노드가 가지고 있는 자식 노드의 수가 가장 많은 차수를 말함)

🥕조건 07 (중요도 🌟 🌟🌟)
Depth : 노드에서 루트까지의 edge 수
Height : 루트 노드와 가장 먼 leaf 사이의 edge 수
Level : depth + 1

depth of a node : root -> each node의 edge의 수(나뭇가지의 수)
🌟depth of a tree(height) : root -> 가장 깊은 node까지의 edge 수
width of a tree : 각 계층에서 node의 최대 node 수

🌲 Tree의 종류

🍃 Binary Tree(이진 트리)

🍃 Non-Binary Tree

🌲 이진 트리

🍃최대 자식의 수가 2임
🍃차수가 2임

🔸이진 트리 특징 (중요도🌟🌟🌟)

i번째 레벨의 최대 노드 수 : 2^(i-1)  (각 계층의 2의 제곱임)
깊이가 k인 이진 트리의 최대 노드 수 : 2^k - 1

🔸이진 트리의 종류

🌲포화 이진 트리
- 모든 노드가 0개 또는 2개의 자식 노드
- 모든 내부 모드는 두개의 자식 노드를 가져야함
- 모든 리프 노드는 동일한 깊이에 있어야함
- 모든 레벨의 노드가 모두 차있는 트리
- 노드의 수 = 2^depth - 1

🌲완전 이진 트리
- 마지막 레벨을 제외한 모든 레벨이 완전히 채워져있고
- 마지막 레벨의 노드들은 왼쪽에서 오른쪽으로 채워진 트리
(레프트차일드랑 라이트차일드가 다 있어야 됨. 라이트차일드만 있으면 완전 이진트리가 아님)

🌲트리의 순회
Search == Traversal (탐색 == 순회)
- 어떠한 값이 주어졌을 때 해당 값이 일치하는 노드가 있는지 보는 것
- 즉 모든 노드를 봐야함

🔸순회방법

🍎Depth-first search (DFS) (깊이 우선 탐색)

- 계층 순서대로 탐색 (할아버지 - 아버지 - 나)

- 트리의 한 경로를 끝까지 탐색한 후 다른 경로를 탐색하는 방법

- 스택, 재귀 이용하여 구현함

▼이진트리는 특히 세가지 방법으로 구현할 수 있음▼

🥕 Preorder Traversal (전위순회) (A - B - C) (루트 -> 왼쪽 -> 오른쪽)

👉A B D H I E C F G

---

🥕 Inorder Traversal (중위순회) (B - A - C) 왼쪽 -> 루트 -> 오른쪽

👉H D I B E A F C G

---

🥕 Postorder Traversal (후위순회) (B - C - A) 왼쪽 -> 오른쪽-> 루트

👉H I D E B F G C C A



💡전위, 중위, 후위가 헷갈리다면?  >>> "루트"에 집중할 것!
- 전위는 루트 > 왼쪽 > 오른쪽
- 중위는 왼쪽 > 루트 > 오른쪽
- 후위는 왼쪽 > 오른쪽 > 루트

 🍎Breadh-fist search (bfs) (너비)

- 계층별로 탐색 (나랑 금쪽이 계층, 아버지 형제들 계층, 할아버지 형제들 계층)

- 트리의 레벨순으로 노드 탐색

- 큐를 이용하여 구현함

📕자료구조 및 알고리즘 (1-1~1-7)

.isalpha() : 알파벳인지 확인

string.ascii_lowercase : A~Z까지 알파벳순으로 소문자로 나열됨

ord : 문자(알파벳 대소문자) → 숫자로 바꿔줌.

점근 표기법 : 알고리즘의 성능을 수학적으로 표기, "효율성"을 따짐

• 빅오 표기법
• 빅오메가 표기법 (이건 거의 안 씀)

시간 복잡도란? 입력값과 문제를 해결하는 데 걸리는 시간과의 상관관계

💡

파이참 디버거 : 내가 원하는 부분만 실행할 때

숫자 앞에 중지 버튼 누르면 실행하지 않음

Run 누르지 말고 Debug 눌러서 실행

중요도: 🌟🌟🌟

stack : 처음 순서에서 반대의 순서로 꺼낸다. (Ctrl + Z 되돌리기 기능과 같음)
#push, pop, empty